Amortized Analysis
Worst-case analysis can be too pessimistic…
In a sequence of operations the worst case does not occur often in each operation — some operations may be cheap, some may be expensive Therefore, a traditional worst-case per operation analysis can give overly pessimistic bound. For example, in a dynamic array only some inserts take a linear time, though others — a constant time. When different inserts take different times, how can we accurately calculate the total time? The amortized approach is going to assign an “artificial cost” to each operation in the sequence, called the amortized cost of an operation. The amortized cost per operation for a sequence of n operations is the total cost of the operations divided by n. It requires that the total real cost of the sequence should be bounded by the total of the amortized costs of all the operations. Note, there is sometimes flexibility in the assignment of amortized costs.
— Victor Adamchik
Amortized Analysis is used to analyze fast operations, where it's occasionally (less frequently) getting slower.
Here, we analyze a sequence of operations and guarantee a worst-case average time. This value is lower than the worst-case time of expensive operation.
Think of a scenario where you are analyzing the expenses for your vehicle.

In one month it's very high due to the insurance renewal payment. For 2 months (2 times a year) it's high because of vehicle service. But if we get a worst-case scenario based on the month where we pay for insurance and service. But the benefit of that insurance is experienced throughout the year. It will be 16 times like a normal month. This is very pessimistic.
Dynamic Tables
Let us consider an example of a simple hash table insertion. How do we decide on table size? There is a trade-off between space and time, if we make hash-table size big, search time becomes fast, but space required becomes high.
The naive solution is to allocate the largest possible space.
The better solution to this trade-off problem is to use Dynamic Table (or Arrays).The idea is to start with a small table and increase the size of the table whenever it becomes full. The following are the steps to follow when the table becomes full.
1. Allocate memory for a larger table of size, typically twice the old table.
2. Copy the contents of the old table to the new table. (expensive operation)
3. Free the old table.
If the table has space available, we simply insert new items in available space. This process in known as table resizing in amotized analysis.
Table Resizing in nutshell
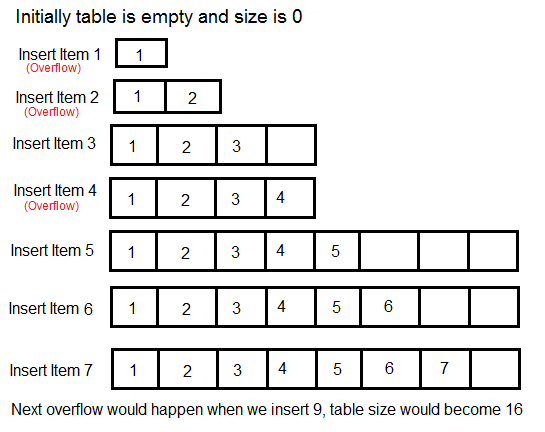
In data structures like dynamic table(array), heap, stack, hashtable (to name a few) we used the idea of resizing the underlying array, when the current array was either full or reached a chosen threshold. [1]
During resizing we allocate an array twice as large and move the data over to the new array. So, if an array is full, the cost of insertion is linear; if an array is not full, insertion takes a constant time. To derive an amortized cost we start with an array of size 1 and perform n insertions.[1]
Techniques in Amortized analysis
Aggregate Analysis
This is what we discussed earlier. Average cost per operation is calcualted(total/n).
Accounting Method
Let say you are maintaing a bank account, Bank charges some amount on each operation. The amount charging is called Amortized cost. So if their is a remainder from past opearation cost, bank carry forward that balance as a “prepaid credit”. So its getting accumilated over time. When there is an expensive operation bank is using that prepaid cost. Thus the total amortized cost provide an upper bound on the total true cost.
Potential Method
Similar to accounting method.
But here , it derives a function characterizing the ‘’capacity’’ for a data structure to be transformed as each operation is performed. This potential either increases or decreases with each successive operationl, but cannot be negative.
References
[1]Amortized Analysis by Victor Adamchik
